(week 5 continued)

Addition:

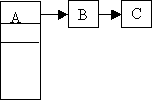
Additions are made to the end of the file.

end of file

prime area

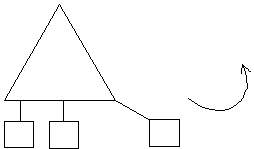
Deletion:

1. Only one record associated with the prime data area.

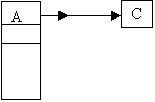
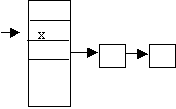Mark the position of record x as available.

2. Deletion of A from the following file

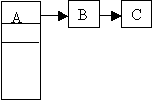
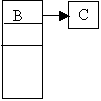
3. Deletion of B from the following file

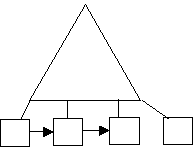
Top-module for deletion:

open input trans-file

open I-o master file

move o to end-of-trans-file

perform

apply-transaction

until end-of-trans-file = 1

close file

stop run

Apply – transaction

A – perform addition operation

D – perform delete operation

M – perform modification operation

perform read-trans-file

Delete operation

Move T_k to input-of-hash-function

Perform hash-function

Perform output-of-has-function to record-position

Perform check-existence

Case of record-states

: not found: error

: found: perform take-out-record

end-of-case

Hashing Techniques For Extendable Hashing

Files expand and shrink as we add and delete records.

B⁺ trees index

data nodes

index data nodes (buckets)

Extendible File

B⁺ trees

90^o

H(K) = pseudo key index (binary number) data bucket

We have:

2 disk accesses: index, data bucket

1 disk access: keep index in main memory only one disk access and it is for the data bucket

number of

index entries index depth

2 1

4 2

8 3

16 4

… …

n log₂ⁿ

Use the leftmost (most significant) n bits (n = depth of index) of the pseudo key to select the corresponding index entry.

directory depth (d)

bucket depth (p): number of bits needed to distinguish the pseudo key on a page from those on other pages.

Example for Extendible Hashing:

Insert 46:

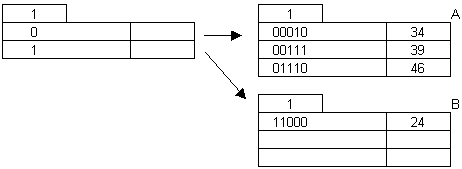
Insert 70:

Insert 7:

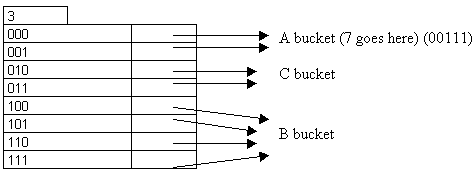
Insert 61:

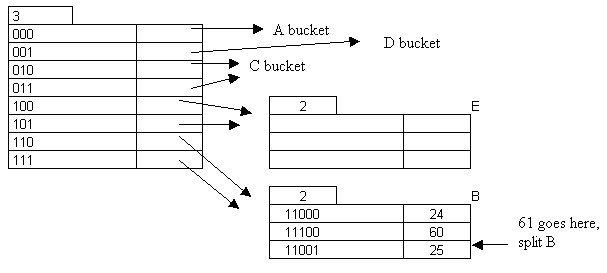
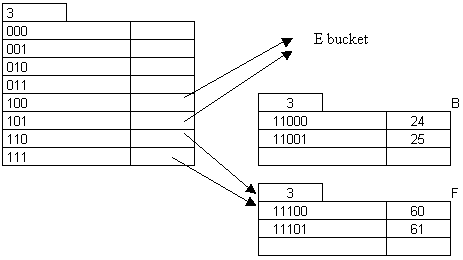
Example: Directory Size

n=6000000(400 bytes/record)

Bkfr=50(Bucket size= 50*400=20kb)

Lf=0.7   6000000/(50*0.7)=171429 buckets (<218)

No of pointers =218

4 bytes/ pointer

218*22=220=(1 MB)

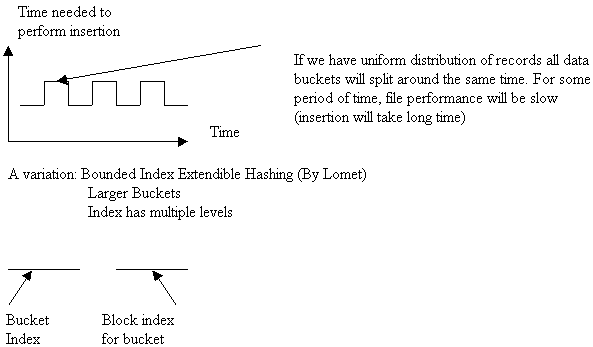
A variation: Bounded Index Extendible Hashing (By Lomet)

         Larger Buckets

         Index has multiple levels

The forest of binary trees is used in dynamic hashing.

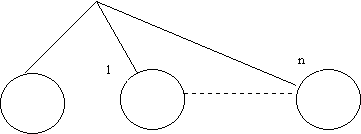
H₀ 0

H₁

Binary trees

H₀(key_i) {0,…n} which subdirectory to use out of(n+1) subdirectiries.

B(H₁ (key_i)) =( b_i0, b_i1, …) b_ij Î {0,1} for all j.

It generates a sequence of binary digits when number of 0’s and 1’s are the same.

This type of binary tree is called “complete binary tree.”

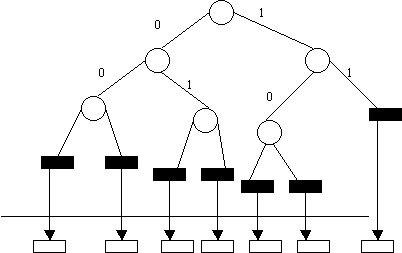(INDEX)

MEMORY

DISK

:Internal node

:External Node(on any level)

:Data Buckets

Internal Node Structure External Node Structure

H₀ (key)=mod(key,3)

H₁ (key)=mod(key,11)

B(0)=1011 B(6) =0001

B(1)=0000 B(7) =1110

B(2)=0100 B(8) =0011

B(3)=0111 B(9) =0111

B(4)=1111 B(10)=1001

B(5)=0101

1.)Insert the records with the keys (27, 42, 11, 37, 14, 30) using dynamic hashing with H₀(key)= mod(key, 3), and H₁(key)= mod(key, 11). Assume that a page (bucket) can hold two records and use the following pseudo random bit string:

(0)= 1011, B(1)= 0000, B(2)= 0100, B(3)= 0110, B(4)= 1111, B(5)= 0101,

B(6)= 0001, B(7)= 1110, B(8)= 0011, B(9)= 0111, B(10)= 1001.

Answer:

Key H₀ (key) H₁ (key) B(H₁ (key))

27 0 5 0101

18 0 7 1110

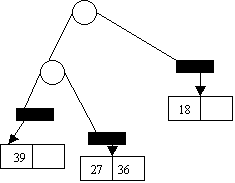
29 2 7 1110

28 1 6 0001

39 0 6 0001

13 1 2 0100

16 1 5 0101

36 0 3 0110

initial condition

H₀ (key)

0 1 2 Subtree 0,1,2 only external nodes

insert 27 insert 18,29,28

0 1 2

Insert 39,13

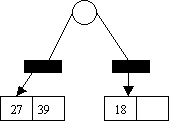
1 1 2

0

Insert 16 1 2

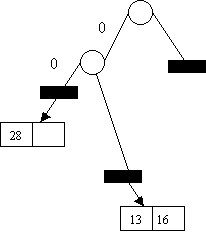
0 1

0 1

1

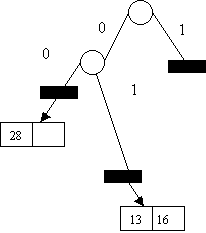Insert 36 1 2

0

0 1

0 1

Index can be too large.How to decrease the index size?

Two variants by Scholl(in ACM TODS)

a)Use overflow buckets to delay splitting

b x Bkfr =no.of records

Bkfr=2

b x Bkfr

0 Overflow bucket

b x Bkfr

Max 3 records =1.5 X 2

Try to insert 4^th one then split

Choose b such that index fits into memory.

The no.of disk accesses is at most éb ù .

b) split the least recently split page after a fixed number of records

No need for pointers. Index size becomes smaller by this we may keep it in memory . so far each record there will be one disk access.(for overflows not one.)

1.) Insert the records with the keys (27, 42, 11, 37, 14, 30) using dynamic hashing with H₀(key)= mod(key, 3), and H₁(key)= mod(key, 11). Assume that a page (bucket) can hold two records and use the following pseudo random bit string:

B(0)= 1011, B(1)= 0000, B(2)= 0100, B(3)= 0110, B(4)= 1111, B(5)= 0101,

B(6)= 0001, B(7)= 1110, B(8)= 0011, B(9)= 0111, B(10)= 1001.

Answer:

Key H₀ (key) H₁ (key) B(H₁ (key))

27 0 5 0101

42 0 9 0111

11 2 0 1011

37 1 4 1111

14 2 3 0110

30 0 8 0011

Initial condition

0 1 2

Insert 27:

0 1 2

Insert 42:

0 1 2

Insert 11:

0 1 2

Insert 37:

0 1 2

Insert 14:

0 1 2

Insert 30:

0 1 2

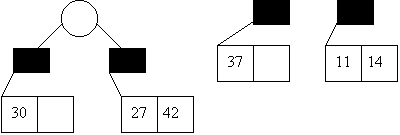
0 1

2.) Redo the above question with the deferred splitting b =1.5

Answer:

The number of records with the overflow area is bX Bkfr = 1.5 X 2 = 3

initial condition

H₀ (key)

0 1 2

insert 27,42,11,37,14

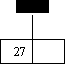
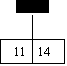
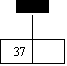0 1 2

insert 30

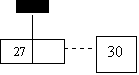
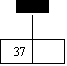0 1 2

Overflow area

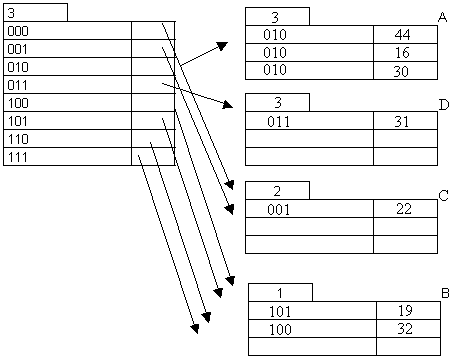
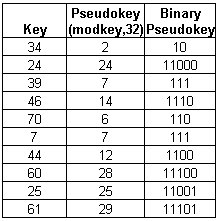
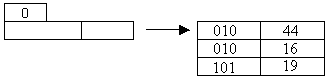
3).Insert the following keys into an extendible hash file:( 44,16,19,30,22,32,31), use bucket size of 3. Hash function is defined mod(key,7).

Answer:

Key	Pseudokey mod(key,7)	Binary Pseudokey
44	2	10
16	2	10
19	5	101
30	2	10
22	1	1
32	4	100
31	3	11

Insertion of 44,16 and 19:

Insertion of 30: 30 (010) goes to A; since A is full, we need to split.

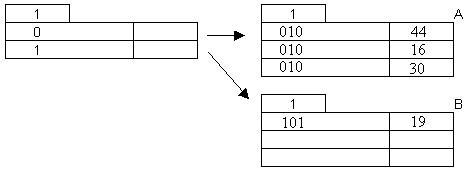
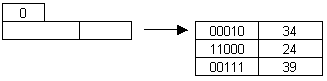
Insertion of 22 and 32: 22 (001) goes to A; since A is full again, we need to split.

32 (100) goes to B.

Insertion of 31: 31 (011) goes to A; since A is full again we need to split.