CREATING
A NEW FILE:

EXHAUSTIVE READING IN ORDER OF A
FIELD:

For the hospital file, it requires
194 hours>8 days
REORGANIZING A SEQUENTIAL FILE:
Why? The file may contain many deleted records.
(Note that when we delete records, we mark them as deleted, but they stay in
the file.)
b(number of blocks) Ή n(number of records)/Bfr(blocking
factor)

REORGANIZING WITH TWO DISK DRIVES:
TY = b * ebt
Assumes that reading and writing are
overlapped.
HOW TO CREATE AN INTERSECTION FILE?
n=100000
R=400 bytes
40 MB
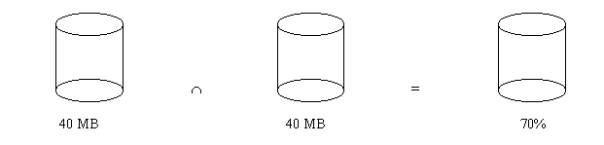
Assume that 70% of the records of F1 & F2 are common.
Method 1:
Read from F1 one by one and search F2 for the record read.
Method 2:
1. Read a large segment of records from
F1 (10 MB).
2. Compare each record in memory with
all records in F2.
Read F1 in terms of 4 segments.
4 seek time + 4 rotational latency
time= 4*(16+8.3)= 97 ms. (negligible)
To read 40 MB, 14 seconds is needed.
To write out the common records,
0.7*14= 10 seconds is needed.
14+10=24 sec.

EXAMPLES :
- Suppose
that a bank has 300 000 records each of which belongs to the individual
customers. If the record size is 200 bytes, what will be the time to read
through the entire file with independent fetches (time for exhaustive
reading of the file)? (Block size for IBM 3380 is 2400 bytes and ebt is
0.84 ms.)
Answer:
Bfr = 2400 bytes/200 bytes =
12
Tx
= n*TF = n*[(n/Bfr)/2]*ebt = 300 000*[(300 000/12)/2]*0.84
= 3 150 000 000 ms. = 3 150 000 sec. ? 36.5 days
- Suppose
that we have two unordered sequential files records of which again
belonging to customers. This time, however, distinct piles belong to
distinct banks. Our aim in this question is to make the file belonging to
common customers of these two banks. In other words, we are going to make
the intersection file of these piles. Some additional information about
the question can be listed as follows:
·
Each
of the unordered sequential files are composed of 300 000 records.
·
60 000
of these records (20%) are common in both files.
·
Both
of the files have 40 MB of data.
So, what is the time
required to make the intersection file?
Answer:
There
are two methods for making intersection files. However, as the second one is
more efficient than the first one, we will use this one.
First
thing to do is to split the data of F1 into 4 smaller segments each
of which are 10 MB. Then comes reading the first segment into the memory and
compare each record in memory with the records in F2. This process
is repeated for all of the 4 segments.
![]() 4 seek time+4 rotational latency time= 4*(16+8.3)=97
ms. (negligible)
4 seek time+4 rotational latency time= 4*(16+8.3)=97
ms. (negligible)
In order to read 40 MB, we need 14 seconds.
To read the common records, we need
14*0.2=2.8 sec.
Then total time is, T.T. = 300 000*7+60
000*14= 2 940 000 sec. = 34 days
SORTED SEQUENTIAL FILES:
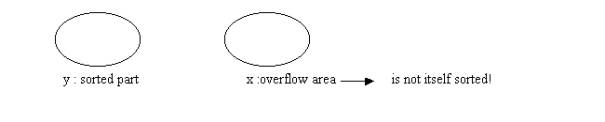
y: number of sorted blocks
x: number of blocks in the overflow area(pile)
x + y : total number of blocks ( x + y = b ) (b denotes the number of blocks)
To find a record, one looks first in the main area. If the record is not in the main area, one searches the overflow area. If only a few records are in the overflow area, operations will take almost the same time as in a fully sorted file. But the sorted file will begin to look like a pile as more and more records are added.
Fetching one record:
To fetch one record, given the value of the field used for sorting, we can do a binary search. We look first at the middle block of the file. If the value we want comes before the values in the middle block, we look at the middle block of the first half of the file. If the value we want comes after the values in the middle block of the file, we look at the middle of the second half of the file. We keep cutting the file in two until we find the record we are looking for or else are left with one block and it does not contain the record we are seeking. At this point, we must search linearly through the overflow area.
Suppose that the record we want is in the original sorted area, then the average number of random accesses is:
Number of accesses= (1/y) * 1 + (2/y) * 2 + (4/y) * 3 + ..+ (1/2) (log y) = log y -1
(Note that the logic is the same as the logic of finding number of accesses in ordinary sequential files)
Then the time if the record is in the sorted area is
[ (log y) 1] * ( s + r + btt )
And the time if the record is in the overflow area is
[ log y] * ( s + r + btt ) + s + r + (x/2)*ebt
The second formula shows the time for the unsuccessful binary search through the sorted area { (log y) * ( s + r + btt ) } , a seek (s) and rotational latency (r) to find the overflow area and a linear search through the overflow area{ (x/2)*ebt }.
y/b : probability that the record is sorted in sorted part
x/b : probability of having the record in the overflow area
Then, the time to fetch of a present record is
TF = (y/b) * [ (log y) 1] * ( s + r + btt ) + (x/b) * [ log y * ( s + r + btt ) + s
+ r + (x/2)*ebt]
If the overflow area is
a. insignificant : TF = (x/b) * [ log y] * ( s + r + btt ) + s + r + (x/2)*ebt
b.
significant : TF = [ (log b) 1] * ( s + r + btt ) since y is nearly b
Example: Let us suppose that we have the hospital file of 40 MB in 16.667 blocks. Then the time to fetch a record is (assume that the overflow area is small)
TF = [ (log b) 1] * ( s + r + btt ) = [ (log 16.667) 1] * ( 16 + 8.3 + 0.8 ) = 326 ms
If 10.000 records are read in logical order, then : 10.000 * 326 = 54 minutes are needed!
Fetching the next record:
To calculate TN, we need to consider two possible conditions: 1. the probability of the next records being in the same block with the recently read record.
2. the probability that it is not in the same block.
The 2nd condition is possible only when the recently read record is the last record of its block. Therefore, the probability of this is 1/(number of records in the block) that is 1/Bfr. Thus, the probability of the first condition is 1-(1/Bfr).
The estimated time for the 1st condition is 0 because of being in the same block and the estimated time for the 2nd condition is ebt since time is needed to read a gap and record.
Thus;
TN = [1-(1/Bfr)]*0 + (1/Bfr)*ebt = (1/Bfr)*ebt
Deleting and modifying records:
TD = TU = TF + 2r as we calculated before!
Inserting a record:
TI = s + r + btt + 2r
( s + r + btt ) denotes the time to access the last block of overflow area and 2r denotes the time to write the new comer to there!
Exhaustive reading of the file:
TX = b * ebt as we calculated before!
EXERCISES:
1. Calculate the time to fetch a record ( TF ) and the time to fetch the next record ( TN ) for the given file:
Number of blocks in the sorted segment (y) : 20.000
Number of blocks in the overflow area (x) : 10.000
Bfr : 10
Assume that we use IBM 3380.
Answer:
Number of block (b) = x + y = 10.000 + 20.000 = 30.000
y/b = 20.000/30.000 = 2/3
x/b = 10.000/30.000 = 1/3
a. TF = (y/b)
* [ (log y) 1] * ( s + r + btt )
+ (x/b) * [ log y] * ( s
+ r + btt ) + s + r + (x/2)*ebt
= 2/3 * 3.3 * (16 + 8.3 + 0.8 ) +
1/3 * 4.3 * (16 + 8.3 + 0.8 ) + 16 + 8.3 + 5.000 * 0.84 ms
= 55.22 + 35.98 + 4224.3 ms
= 4315.5 ms
= 4.3 sec
b. The time to fetch
the next record I it is in the sorted part is
TN
= (1/Bfr) * ebt
= 1/10 * 8.4 ms
= 0.84 ms
If it is in the overflow area, we must first establish that it is not in
the sorted area by fetching the next block if necessary; then we must do a
sequential read of the overflow area. We get
TN
= (1/Bfr) * ebt + (x/b) * [ s + r + (x/2)*ebt ]
= 1/10 * 8.4 + 1/3*(24.3 + 5.000*0.84)
ms
= 1408,94 ms
= 1.4 sec
EXTERNAL SORTING:
Sorting & Searching by Donald Knuth.
- When do we need external search for a file? When the file is too large.
- How do we do external search? First, we form sorted segment, then we merge them.
If we have only one disk drive, we use heapsort to create the initial sorted segments. Unlike most other sorting routines, heapsort can be executed overlapping the input and output. That is, only I/O time needs to be counted.
With two
disk drives we can use a variation of heap sort called replacement selection.
With replacement selection, the resulting initial sorted segments are twice the
size of available memory. Additionally, the reading in of the unsorted file and
the writing out of the sorted segments overlap. Thus, the initial stage of
sorting takes essentially the time to write the file once.
Overlapping heapsort with I/O:
Definitions:
Complete binary tree: a
tree which has all of its leaves on 2 levels, the kth level and
(k-1)th level, and the leaves on the bottommost or kth
level are in the left most position in that level. Nodes above the kth level
have exactly two children each.
Heap (Priority Queue) : a complete binary tree where each node
contains a record with a key value which is smaller than the keys in its two
children.
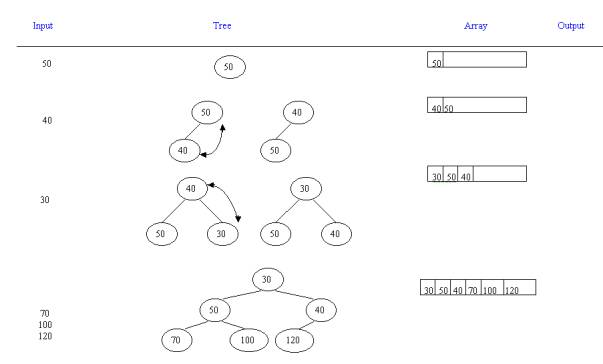
Insertion into a Heap:
While we have enough space
1. Obtain the next record from the current input buffer.
2. Put the new record at the end of the array (i.e., make it the rightmost node on the bottom level of the tree)
3. If the key of the new record is smaller than the key of its parent. Exchange the new record with its parent. Repeat this until heap property is satisfied.
Analysis & Observations:
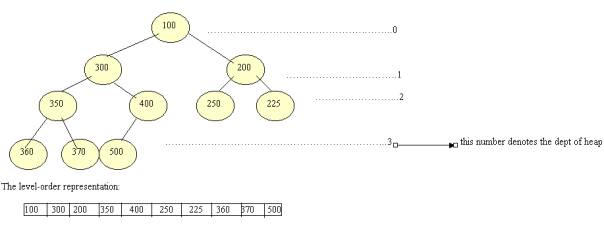
1. When we arrange in level-order, the children of the ith element in the array are in the 2ith and the (2i+1)th elements of the array. This makes heapsort easy to program.
2. Depth of tree : λlog2 nϋ for n number of records.
3. Step 2 of the algorithm £ log2 n
Example:
If we have 400-byte records in a 2400 byte block, we must perform six insertions while reading in the next block ( since Bfr = 2400/400 = 6 ). If there are 10MB in each segment, there will be nearly 25.000 records in the tree ( since 10MB consists of approximately 25.000 400-byte records ) towards the end of the construction process. The log (base 2) of 25.000 is between 14 and 15.
14< log2 25.000 < 15
This means each record insertion causes at most 14 exchanges. Each block has six records. Thus, in the worst case, about 84 (6*14) comparisons and exchanges must be performed while the next block is being read in. If the execution step of each one takes about 10 microseconds, then 0.84 ( 10*84 /1000) milliseconds is needed.
EXERCISES:
- Given a file
Record size: 400 bytes
Block size: 2000 bytes
File size : 20 MB
If the execution of each block takes 20 microseconds, find the time needed to form the heap.
Answer:
Bfr = 2000/400 = 5
Number of records = 20.106 / 400 =50.000
15 < log2
50.000 < 16
Then, at most 15 comparisons are needed for one record
insertion.
15 * 5 = 75
comparison for each block insertion.
75 * 20 = 1500 microseconds = 1.5 milliseconds
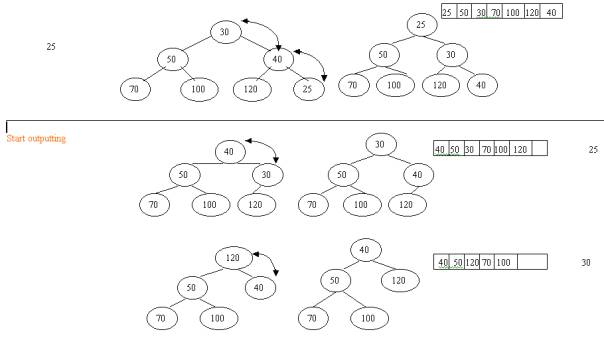
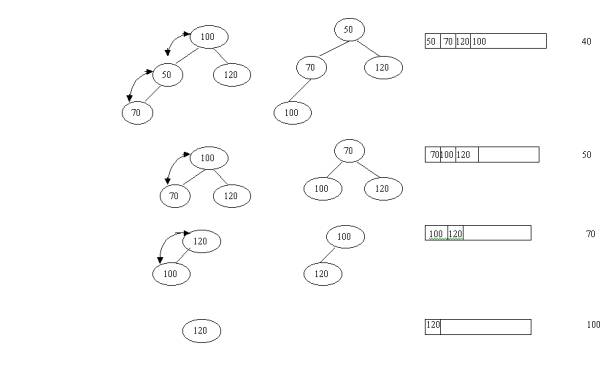
OUTPUT A HEAP (CREATE A SORTED FILE SEGMENT)
While we have more
records in a tree which have not been written to disk, repeat the following:
- Put the root
record in the current output buffer. Put the rightmost bottom record in
the root position. Call it x.
- (Restore Heap Property) compare the key
value of x with the keys of its two children. If the key value of x is not
smaller, then exchange it with smaller of its two children. Repeat the
step for x in its new position. When x is smaller than both of its
children, stop.
Example:
A heap output with array size 7. In this
illustration we have memory space for seven records. We read in seven records, inserting
them into the heap. Then we begin writing out the sorted seven-record segment.

EXECUTION TIME
Ignore CPU since it is overlapped I/O time. We have b number of blocks in the file. First read all blocks (b blocks) one by one. Then write them( b blocks) back to disk after sorting.
Therefore, total execution time is 2b*ebt.
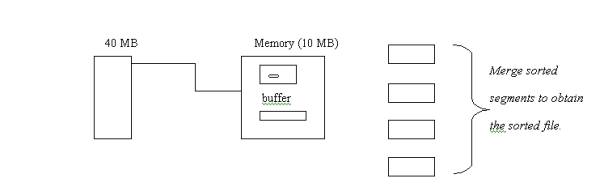
ONE DISK DRIVE LARGE MEMORY MERGING
Now we are working with a hypothetical disk drive, which has room for both the sorted and unsorted 2400-megabyte file, has only one disk arm, but has all the parameters of the IBM 3380. How fast can we sort this file? We assume as usual that the memory capacity available is 10 MB.
We first try a two-way merge. This means that we merge two of the segments at a time. Since the memory only contains 10 MB, we cannot read two segments into memory at once. Instead we read half of one segment (5 MB) and half of another segment (another 5 MB) into memory first. That is, we have 5 MB buffers for each input file. Since we have only one disk arm, we cannot overlap reading with writing or reading one segment with reading another segment. After the 5 megabytes from each input segment is separately loaded, we can overlap writing out with merging using simple double buffering of the output segment. When one f the input buffers is exhausted, we stop output and read in the second 5 megabyte half of the segment. We resume merging and writing. The time for merging two sorted segments (each with seg blocks) is:
(4+3)*(r+s)+2*2*seg*ebt
EXERCISES:
1. Produce a sequence of keys for records, which will yield a sorted segment of 18 records with only a 7-record memory capacity when replacement selection is used. What if we want 18 records such that exactly 9 will go out in the first segment and 9 in the second also with a 7-record memory capacity?
Answer:
For the first option,
use a sequence of 18 numbers, which are already sorted. For the second option,
create a sequence of numbers for keys for the first 9 records, which are all
larger than those of the second 9 records. The point is that new comers join
the old heap only as long as their keys are larger than those written out.
2. Calculate the time to sort an 8-megabyte file with one disk drive and 10 megabytes of memory. Note that the number or size of the records does not matter.
Answer:
An 8 MB file is 8*220
bytes long, which means that there are3333 blocks of 2400 bytes each. The time
to read and write this file is 2b*ebt, which is equal to 2*3333*0.84=5599
ms=5.6 sec