LectureNotes, Week 2
Prepared by: Nurettin Mert Aydın /Ahmet Örnek /ArmağanDurusal
I/O Time in Disks
We
assume that there is just a single user for the system and ignore the CPU
time (it is negligible).
Block
Transfer Time (btt):Time
needed to read block to memory (buffer)
3600/60 = 60 rev./sec. => 1/60 sec./rev. (It takes 1/60 seconds to complete 1 revolution)
1/60
sec/rev = 1000/60 msec/rev = 16.67msec/rev
r
= f (revolution time) / 2 =>
r = 16.67/2 ~ 8.3 msec/rev
Units and Specifications of IBM 3380
Size = 2500 MB
Random vs. Sequential Reading
With the information of IBM 3380,sequential and random readings can be calculated as in the following table:
|
Read Type
|
10 Blocks to Read
|
100 Blocks to Read
|
|
|
Sequential
|
s
+ r + 10 * ebt
=
16 + 8.3 + 10 * 0.84
=
32.7 msec
|
s
+ r + 100 * ebt
=
16 + 8.3 + 100 * 0.84
= 108.3 msec |
|
|
Random
|
10
* (s + r + btt)
=
10 * (16 + 8.3 + 0.80)
= 251 msec |
|
Let"b" denote the number of blocks to be read
Random Read : b * ( s + r + btt)
Note:
In our calculations we assume that blocks are even multiple of record size
Bfr
(blocking factor)=B
(Block size) / R (Record size)mod
(B,R) = 0
b
(number of blocks) = n (number ofrecords) / Bfr
Example(COBOL):
In
data division of COBOL programs:
RECORD
CONTAINS80 CHARS
BLOCKCONTAINS10 RECORDS
Here, BLOCK indicates a BUCKET
bk: numberof buckets
r: rotational latency time
s: seek time
dtt:
data transfer time
time = bk * (s + r + dtt)
= bk * (s + r) + bk * dtt
Let
"bk * (s + r)" be the first component. We are calculating the total
of seek time (s) and rotational latency time (r) for each bucket (by multiplying
this total time by the number of buckets). This component depends on the
bucket size.
Let
"bk * dtt" be the second component. This component is independent
from the bucket size. Whatever the bucket size is, some amount of data
will always be read.
When we increase the total size, random read time decreases.
When we decrease the total size, random read time increases.
Random
Read Time of the Records in a File
This
approach assumes that we have (in memory) a list of records in the file
as well as their corresponding addresses.
n
: numberof records
time
= n * (r + s + dtt)
When we increase the bucket size, this I/O time increases.
When
we decrease the bucket size, this I/O time decreases.
Example:
n = 30.000
record size (bytes/record) = 100 bytes
block size= 2400 bytes
btt (blocktransfer time):
a) for random = 2400/3000 = 0.8 ms
b) for sequential = 2400/2857 = 0.84 ms.
|
|
|
(of all buckets) |
(by record) |
(by bucket) |
| 2400 |
(30000
* 100)/2400
=
1250
|
1250
* 0,84
=
~ 1 sec
(r,
s ignored)
|
30000
* (16 + 8,3 +0,8)
=
753 sec
where
16 = r, 8,3 = s
|
1250
* (16 + 8,3 + 0,8)
=
31 sec
|
| 4800 |
(30000
* 100)/4800
=
625
|
625
* (0,84 + 0,84)
=
~ 1 sec
|
30000
* (16 + 8,3 + 1,64)
=
778 sec
where
1,64 = 0,8 + 0,84
|
625
* (16 + 8,3 + 1,64)
=
16 sec
|
| 14400 |
(30000
* 100)/14400
=
208.33
|
208,33
* (0,84 * 6)
=
~ 1 sec
|
30.000
* (16 + 8,3
+ 0,8 + 5*0,84)
=
879 sec
|
208,33
* (16 + 8,3
+ 0,8 + 5*0,84)
=
6 sec
|
| 28800 |
(30000
* 100)/28800
=
104.16
|
104,6
* (0,84 * 12)
=
~ 1 sec
|
30.000
* (16 + 8,3
+ 0,8 + 11*0,84)
=1030
sec
|
104,16
* (16 + 8,3
+ 0,8 + 11*0,84)
=
3,6 sec
|
| ... | ... | ... | ... | ... |
|
as the size increases
|
decreases | no effect | little effect | makes a significant difference |
[Above in the table, in random reading, we used 1,64 and this is the total of a single random reading time (0,8) followed by a seq. reading time (0,84).
Optimum Bucket Size for a Mix of Operations
For the file described in the example above,
Think of a 1000 random reads + reading of whole file by bucket
What is the optimum bucket size (x)?
1000 * (s + r + dtt) + bk * (s + r + dtt)
where "1000 * (s + r + dtt)" is "1000 random reads"
and "bk * (s + r + dtt)" is "all of the buckets read"
=(1000 + bk) * (s + r + dtt)
dtt= bucket size / t' where t' = 2857
bk= [(number of records)(record size)] / x = [(30.000)(100)] / x
f(x) =[1000 + (3.000.000/x)] [16 + 8,3 + (x/2857)]
Take the derivative with respect to x and set it equal to zero to find x which yields the minimum cost
f(x) =constant + [(24,3)(3.000.000)]/x + [(1000) x]/2857
(24,3)(3.000.000)=
x-2(1000/2857) =>x = 14,431
SEQUENTIAL
FILES
Pile:
unordered sequential fıle
Assumptions: Large file, single user, fixed size records
File
Operation Times
TF= time to fetch (fınd and read) one record
TN= time to fetch next record
TI= time to insert a new record
TU=
time to update a record
TD= time to delete a record
TX= time for eXhaustive reading of a file
TY= time for reorganization of a file
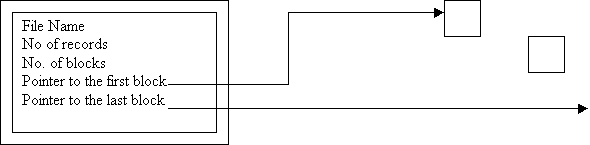
OS(operating system) has a file header (file control block) for each file.The headers include information about the fıle and records and blocks.
file control block

![]()
Extents
are large areas of blocks.A file will be stored in terms of extents.
TF:Fetching
One Record
In the pile file we search sequentially through the whole file until we find our target record.
TF= Single record fetch
12b = no.of blocks
![]()
"blocks", each one has the same chance (1/b) to be selected
average no. of blocks to be read = 1 * 1/b+2 * 1/b+3 * 1/b+..................+b * 1/b=
=(1 + 2 + 3 +..................+ b) *1/b =
=( b*(b+1)/ 2 )*1 / b= ( b+1) / 2» b / 2
TF=(
b / 2) * ebt![]() (sequential
read)
(sequential
read)
Example
(Hospital File)
The file has patient records of a hospital. It has 100 000 records of 400 bytes each. How much will it take to look up the record without using an index.
n = 100 000 ( no. of records)
R = 400 bytes (record size)
B = 2400 bytes (block size)
(no.
of blocks) = b = 105 * 4 * 102 /2400=1.6667
*10 4
b / 2 = 8333,ebt= 2400 / 2857 = 0.84ms
TF= 8333 * 0.84=7000 ms = 7 sec.(for 1 record)
For 10 000 records it will take7 * 104 records~19 hours!
TN:Fetching the Next Record
TN =Time needed to fetch the next (logical) record
It will take the same time as random record fetching because the records in a file are not stored in order.
TN=TF
TI:Inserting a New Record
TI=Time to insert a new record
To insert a new record we place it at the end of the file.
We assume that the address of the last block is kept in memory.Also it can be kept in the file header and replaced at the end of the session.
File header

![]()
![]()
![]()
![]() New
corner
New
corner
Last Block
For insertion the last block is read and the new record is put at the end.
TI=s + r + btt +2r
"s + r +btt" is for the reading of the last block
"2r"is for the waiting time for 1 full revolution to write the block back to its place
e.g. For IBM 3380TI =
42 ms.
During marking the disk revolves back to the original position and after that modified record is written (tombstone approach).
The time to wait for the disk until it rotates back to the original position is 2r-btt and the time to transfer the new record is btt.
TD
= T F + 2r (= TF + 2r - btt + btt)
TU
=TF+2r
TX
= b * ebt
For hospital file in the example
TX=16
667 * 0.84 = 14 000 ms = 14 sec