Chapter 3 - E-R MODEL (continued)
3.5.3 Translating Relationship Sets with Key Constraints
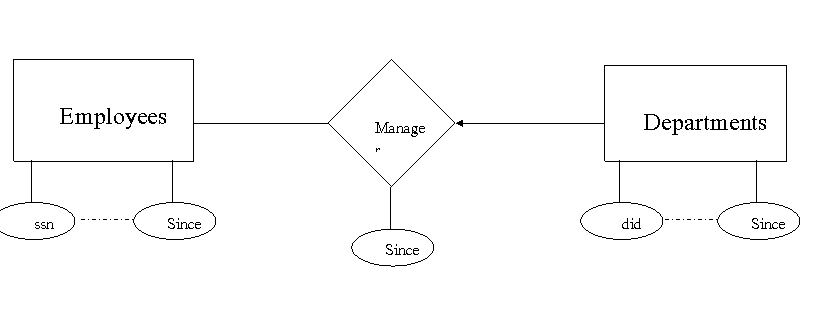
Manager (SSN, did, since)
Manager (did, SSN, since)
One manager - Many departments
SQL:
CREATE TABLE Manager
( ssn CHAR (11),
did INTEGER,
since DATE,
PRIMARY KEY (did),
FOREIGN KEY (ssn) REFERENCES Employees,
FOREIGN KEY (did) REFERENCES Departments)
3.5.4 Translating Relationship Sets with Participation Constraints
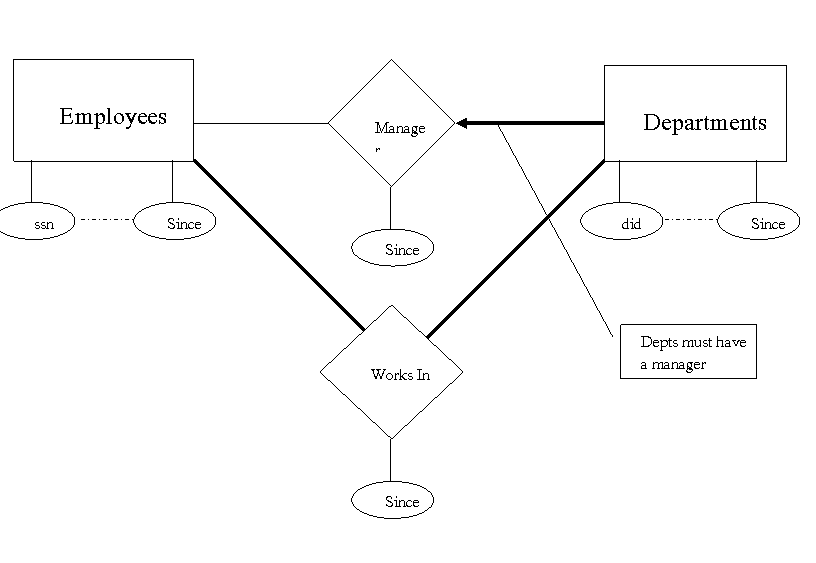
ü Every department is required to have a manager due to the participation constraint and at most one manager due to the key constraint.
SQL:
CREATE TABLE Dept_Manager
( did INTEGER,
dname CHAR(20),
budget REAL,
ssn CHAR(11) NOT NULL,
since DATE,
PRIMARY KEY (did),
FOREIGN KEY (ssn) REFERENCES Employees
ON DELETE NO ACTION)

3.5.5 Translating Weak Entity Sets
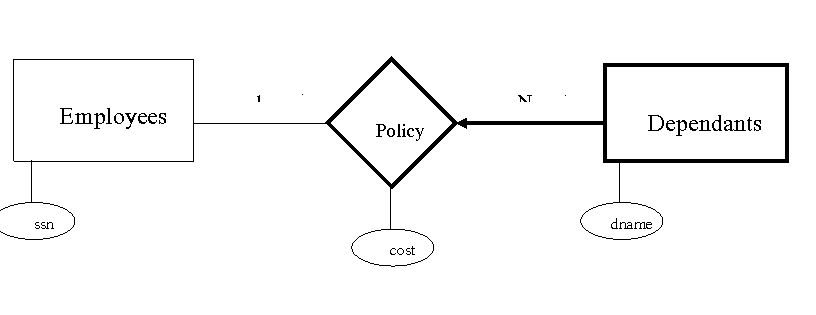
ü Weak Entity is dependant on the other entity.
ü A weak entity always participates in a one-to-many binary relationship and has a key constraint and total participation.
SQL:
CREATE TABLE Dept_Policy
( dname CHAR(20),
age INTEGER,
cost CHAR(11),
ssn CHAR(11),
PRIMARY KEY (dname, ssn),
FOREIGN KEY (ssn) REFERENCES Employees
ON DELETE CASCADE)
3.5.6 Translating Class Hierarchies
]
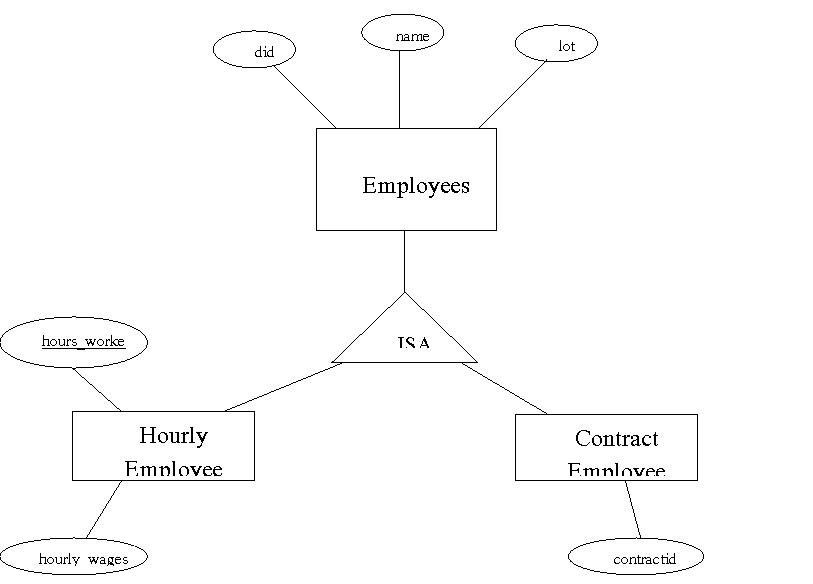
a) Three Relations
 Emp(
ssn, name, age)
Emp(
ssn, name, age)
H_Emp( ssn, hours_worked, hourly_wages)
C_Emp( ssn, contract_id)
b) Two Relations

H_Emp( ssn, name, age, hours_worked,
hourly_wages)
C_Emp( ssn, name, age, contract_id)
Relational Algebra
Arithmetic Operators: +, -, *, /
Operators
Set
Oriented:
È : Ç : Intersection - : Difference |
|
C : Cartesian Product
Relation Oriented:
p : Projection ![]()
s : Selection ![]()
![]() : Join
: Join
![]()
![]()
![]() =
= ![]()
¸ : Division
|
|
|
|
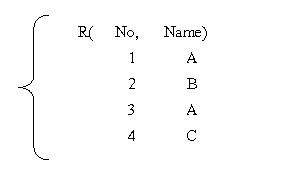
Intersection: R1ÇR2?R( |
No, |
Name) |
1 |
A |
|
3 |
A |
Difference: R1-R2?R( |
No, |
Name) |
2 |
B |
R1 Ç R2 = R1 - ( R1 - R2 )
Cartesian Product : R1 C R2 ? R( |
R1.No |
R1.Name |
R2.No |
R2.Name |
1 |
A |
1 |
A |
|
1 |
A |
3 |
A |
|
1 |
A |
4 |
C |
|
2 |
B |
1 |
A |
|
2 |
B |
3 |
A |
|
2 |
B |
4 |
C |
|
3 |
A |
1 |
A |
|
3 |
A |
3 |
A |
|
3 |
A |
4 |
C |
Employee( |
EmNo |
,Name |
,Status) |
Ü Relation Schema |
||
1 |
Peter |
A |
|
|||
2 |
Mary |
B |
||||
3 |
Jane |
A |
||||
10 |
Ann |
C |
||||
11 |
Peter |
A |
||||
12 |
Mary |
A |
Projection p : ![]()
pName (Employee) ? ( |
Name) |
|||||||
Peter |
|
|||||||
Mary |
||||||||
Jane |
||||||||
Ann |
||||||||
Peter |
||||||||
Mary |
pName, Status (Employee) ? ( |
Name |
,Status) |
Peter |
A |
|
Mary |
B |
|
Jane |
A |
|
Ann |
C |
|
|
|
|
Mary |
A |
Selection ( Restriction)
s : ![]()
sStatus=A (Employee) ? ( |
EmpNo |
,Name |
,Status) |
1 |
Peter |
A |
|
3 |
Jane |
A |
|
11 |
Peter |
A |
|
12 |
Mary |
A |
sStatus=A Ú Status=C (Employee) ? ( |
EmpNo |
,Name |
,Status) |
1 |
Peter |
A |
|
3 |
Jane |
A |
|
10 |
Ann |
C |
|
11 |
Peter |
A |
|
12 |
Mary |
A |
Ú = OR Ù= AND
Question: Find all EmpName’s with status=A
pName (sStatus=A (Employee))
Question: Find all EmpNo’s and EmpName’s with Status=A or Status=B
pEmpName,Name (sStatus=A Ú Status=B (Employee))
Join ( ![]() ) : Equijoin=Condition is explicit
) : Equijoin=Condition is explicit
Natural Join=Condition is implied.
Teta ( Condition) Join, Outer Join (See Chapter 5)
Emp_Part
( |
EmpNo |
,PartNo |
,Quantity) |
1 |
P1 |
2 |
|
1 |
P2 |
3 |
|
2 |
P3 |
1 |
|
2 |
P4 |
2 |
T=Employee ![]() Emp_Part
Emp_Part
(Employee EmpNo = EmpPart Empno)
T
( |
EmpNo |
,Name |
,Status |
, Part No |
,Quantity) |
1 |
Peter |
A |
P1 |
2 |
|
1 |
Peter |
A |
P2 |
3 |
|
2 |
Mary |
B |
P3 |
1 |
|
2 |
Mary |
B |
P4 |
2 |
Question: Find Part No’s and quantities supplied by Employee with status A.
p (Part No, Quantity) (sStatus=A (Employee ![]() EmpPart) )
EmpPart) )
Natural Join: Check the equalities of all fields (attributes) having the same name and in the resultant relation keep only one
of the attributes with the same name.
R1 ( |
A |
,B |
,C) |
|
a1 |
b1 |
c1 |
a1 |
b2 |
c1 |
|
|
a1 |
b2 |
c2 |
a2 |
b1 |
c1 |
|
a2 |
b1 |
c2 |
|
a3 |
b1 |
c2 |
R2 ( |
B |
,C |
,D) |
|
b1 |
c1 |
d2 |
b2 |
c2 |
d1 |
|
|
b3 |
c1 |
d2 |
b3 |
c2 |
d2 |
Find the natural join of R1 and R2 on the common attributes.
R = R1 ![]() R2
R2
R1.C > R2.C
R ( |
R1.A |
R1.B |
R1.C |
R2.B |
R2.C |
R2.D) |
|
a1 |
b1 |
c2 |
b1 |
c1 |
d2 |
a1 |
b1 |
c2 |
b3 |
c1 |
d2 |
|
|
a2 |
b1 |
c2 |
b1 |
c1 |
d2 |
a2 |
b1 |
c2 |
b3 |
c1 |
d2 |
|
a3 |
b1 |
c2 |
b1 |
c1 |
d2 |
|
a3 |
b1 |
c2 |
b3 |
c1 |
d2 |
Division (÷) : Unary relation (One attribute relation.)
R1 ( |
A |
,B) |
|
a1 |
b1 |
a1 |
b2 |
|
|
a2 |
b1 |
a3 |
b1 |
|
a4 |
b2 |
|
a5 |
b1 |
|
a5 |
b2 |
R2(B) |
=> |
R=R1
÷ R2 |
=> |
R(A) |
|
b1 |
a1 |
||||
b2 |
a5 |
R2(B) |
=> |
R=R1
÷ R2 |
=> |
R(A) |
a1, a2, a3, a5 |
b1 |
R2(B) |
=> |
R=R1
÷ R2 |
=> |
R(A) |
|
b1 |
Æ |
||||
b2 |
|||||
b3 |
R2(B) |
=> |
R=R1
÷ R2 |
=> |
R(A) |
a1,
a2, a3, a4, a5 |
Æ |