CS 476 Quizes

1. Date: Feb. 20, 2001.
   Question: Convert the following NFA w/epsilon-moves to an equivalent NFA.

   	d	0	1	e
   ->	A	0	{B}	0
   	B	{D}	0	{C}
   *	C	0	{E}	0
   	D	0	{B}	0
   	E	{C}	0	0

   Answer: NFA:

   	d	0	1
   ->	A	0	{B, C}
   	B	{D}	{E}
   *	C	0	{E}
   	D	0	{B, C}
   	E	{C}	0

   ---

2. Date: Mar. 15, 2001.
   Question: What are the equivalence classes of R_L induced on 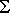={0,1}, where L is defined by the regular expession a(a+b)*b? What is the index of R_L?

   Answer: 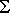*/R_L = {C₀, C₁, C₂, C₃ }, where
   C₀ = e,
   C₁ = a(a+b)*b,
   C₂ = a(a+b)*a,
   C₃ = b(a+b)*.
   The index of R_L is 4.

   ---

3. Date: Mar. 22, 2001.
   Question: Design a CFG for the language {aⁿbⁿc^md^m}. Show the derivation trees of the string abcd in this grammar.

   Answer:

   S -> AB
   A -> aAb | ab
   B -> cBd | cd
   

   The derivation tree:

          S
         / \
        A   B
       /\  / \
      a  b c  d
   

   ---

4. Date: Mar. 27, 2001.
   Question: Convert the following grammar into CNF.

   S -> aBC
   B -> bB | b
   C -> D
   D -> ab
   

   Answer: After the removal of unit productions:

   S -> aBC
   B -> bB | b
   C -> ab
   D -> ab
   

   After the removal of useless symbols:

   S -> aBC
   B -> bB | b
   C -> ab
   

   After replacing terminal with new variables:

   S -> CaBC
   B -> CbB | b
   C -> CaCb
   Ca -> a
   Cb -> b
   

   Equivalent grammar in CNF:

   S -> CaD
   D -> BC
   B -> CbB | b
   C -> CaCb
   Ca -> a
   Cb -> b
   

   ---

5. Date: Apr. 10, 2001.
   Question: Give CFG's for the following languages:
   a) L_a = {a^jb^jc^k | j > 0, k > 0}
   b) L_b = {a^jb^kc^k | j > 0, k > 0}

   Answer:
   a) G_a: S -> AB, A -> aAb | ab, B -> cB | c
   b) G_b: S -> AB, A -> aA | a, B -> bBc | bc

   ---

6. Date: Apr. 17, 2001.
   Question: Design a Turing Machine to accept 0*1*.

   Answer:

   d	0	1	B
   q0	(q0,0,R)	(q1,1,R)	(q2,B,R)
   q1	-	(q1,1,R)	(q2,B,R)
   q2	-	-	-

   F = {q₂}

   ---

7. Date: May 10, 2001.
   Question: Define the language of the problem "Does DFA M accept the string w?" Is this problem decidable?

   Answer: L= { <M,w> | M accepts w}.
   There is an algorithm to determine if a DFA M accepts the string w. The algorithm halts in |w| steps, with Yes or No answer. Therefore, the language L is recursive, and the problem is decidable.