CS 315-01 Quizzes

Date: Sept. 22, 2025
Question: Given the following grammar,

<program> ::= <stmt_list>
<stmt_list> ::= <stmt> | <stmt> <stmt_list>
<stmt> ::= <declaration_stmt> | <assign_stmt> 
<declaration_stmt> ::= var <ident_list> ;
<ident_list> ::= <var_id> | <var_id> , <ident_list>
<var_id> ::=  a | b | c | d | e
<assign_stmt> ::= <var_id> = <expression> ;
<expression> ::= <expression> + <expression>
               | <constant> | <var_id>
<constant> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

a) Drive the string "var a, b, c; a = a + b + 5;", using the rightmost derivation to show that it is in the language.

b) Show its parse tree.

c) Is the grammar ambiguous or not?

Answer:

a) The leftmost derivation:

<program> ⇒ <stmt_list>
          ⇒ <stmt> <stmt_list>;
          ⇒ <stmt> <stmt>;
          ⇒ <stmt> <assign_stmt>;
          ⇒ <stmt> <var_id> = <expression> ;
          ⇒ <stmt> <var_id> = <expression> + <expression>> ;
          ⇒ <stmt> <var_id> = <expression> + <constant> ;
          ⇒ <stmt> <var_id> = <expression> + 5 ;
          ⇒ <stmt> <var_id> = <expression> + <expression> + 5 ;
          ⇒ <stmt> <var_id> = <expression> + <var_id> + 5 ;
          ⇒ <stmt> <var_id> = <expression> + b + 5 ;
          ⇒ <stmt> <var_id> = <var_id> + b + 5 ;
          ⇒ <stmt> <var_id> = a + b + 5 ;
          ⇒ <stmt> a = a + b + 5 ;
          ⇒ <declaration_stmt> a = a + b + 5 ;
          ⇒ var <ident_list> ; a = a + b + 5 ;
          ⇒ var <var_id> , <ident_list> ; a = a + b + 5 ;
          ⇒ var <var_id> , <var_id> , <ident_list> ; a = a + b + 5 ;
          ⇒ var <var_id> , <var_id> , <var_id ; a = a + b + 5 ;
          ⇒ var <var_id> , <var_id> , c ; a = a + b + 5 ;
          ⇒ var <var_id> , b , c ; a = a + b + 5 ;	  
          ⇒ var a , b , c ; a = a + b + 5 ;  ✓

23 sentential forms.

b) The parse tree

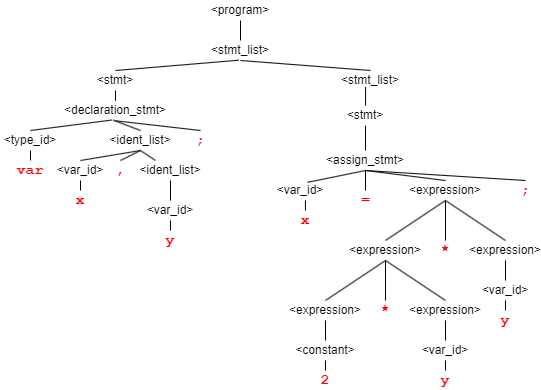
c) It is ambiguous, becuase <expression> ::= <expression> + <expression> rule can be expanded from the left <expression> or the right one leading to two different parse trees.

Date: Oct. 2, 2025
Question: Write a lex file to generate a scanner that will print EU_DATE or USA_DATE, if the input is a string representing a date in European or United States format, respectively. For other strings, it will display NOT_A_DATE.
You may assume the year value is grater than 1000, less than 10000.
Examples of USA date format: 2/19/2019, 10/29/1923, 04/20/1920, 1.2.2025.
Examples of EU date format: 19.2.2019, 29.10.1923, 20.04.2019, 2/1/2025.
Answer:
```
%option main
day    0?[1-9]|[12][0-9]|3[0-1]
month  0?[1-9]|1[0-2]
year   [1-9][0-9][0-9][0-9]
%%
{month}\/{day}\/{year}   printf("USA_DATE");
{day}\.{month}\/{year}   printf("EU_DATE");
.*                       printf("NOT_A_DATE");
```
Date: Oct. 13, 2025
Question: In this quiz, you will write a yacc specification file with tokens corresponding to the unique letters in your first name, only. For example, in my case, the tokens are H, A, L, I.
a) Write the grammar rules in such a way that the grammar will have a shift/reduce conflict if your ID is odd, a reduce/reduce conflict if your ID is even.

b) Indicate on what token the conflict will occur.

c) Is your grammar ambiguous? Why?

Answer:
a) Shift/reduce conflict:
```
%token  H A L I
%%
start: x L | y A I;
x: H A;
y: H ;
```
b) The token causing the conflict is A
c) The grammar is unambiguous. The language of the grammar is L={HAL, HAI}. Each of the words in the language has exactly one poarse tree.
```
        start          start
        /  \          /  |  \
       x    L        y   A   I
      / \            |
     H   A           H
```
Or,
a) Reduce/reduce conflict:
```
%token  H A L I
%%
start: x A L | y A I;
x: H ;
y: H ;
```
b) The token causing the conflict is A
c) The grammar is unambiguous. The language of the grammar is L={HAL, HAI}. Each of the words in the language has exactly one poarse tree.
```
      start          start
     /  |  \        /  |  \
    x   A   L      y   A   I
    |              |
    H              H
```
Date: Oct. 23, 2025
Question:
```
<script>
x = 5;

function foo() {
  console.log("in foo 1, x=" + x);
  x = 7;  // (*)
  console.log("in foo 2, x=" + x);
}

console.log("in global 1, x=" + x);
foo();
console.log("in global 2, x=" + x);
</script>
```
Describe what happens when the code runs,
a) as given above.
b) when the line with (*) is replaced with var x = 3;
c) when the line with (*) is replaced with let x = 3;
Answer:
a) The statement x = 3; is executed as an assignment to the global variable x. The following are written to the console.log. Test the code
```
in global 1, x=5
in foo 1, x=5
in foo 2, x=7
in global 2, x=7
```
b) The statement var x = 3; declares a new local variable x and initializes it to undefined, as the first executable statement in the body of foo. The console.log("in foo 1, x=" + x); statement displays that x is undefined. The following are written to the console.log. Test the code
```
in global 1, x=5
in foo 1, x=undefined
in foo 2, x=3
in global 2, x=5
```
c) The statement let x = 3; declares a new local variable x as the first executable statement in the body of foo, but it does not initialize x. The console.log("in foo 1, x=" + x); statement generates and error message indicating that x is not initialized>, and the execution halts. The following are written to the console.log. Test the code
```
in global 1, x=5
Uncaught ReferenceError: Cannot access 'x' before initialization
    at foo (q4c.htm:7:32)
    at q4c.htm:13:1
```