Question: Given the following grammar,
<program> ::= <stmt_list>
<stmt_list> ::= <stmt> | <stmt> <stmt_list>
<stmt> ::= <declaration_stmt> | <assign_stmt>
<declaration_stmt> ::= var <ident_list> ;
<ident_list> ::= <var_id> | <var_id> , <ident_list>
<var_id> ::= x | y | z
<assign_stmt> ::= <var_id> = <expression> ;
<expression> ::= <expression> + <expression>
| <constant> | <var_id>
<constant> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Drive the string "var x, y, z; z = 3 + x + y;",
using the rightmost derivation to show that it is in the language.
Answer:
The rightmost derivation:
<program> ⇒ <stmt_list>
⇒ <stmt> <stmt_list>
⇒ <stmt> <stmt>
⇒ <stmt> <assign_stmt>
⇒ <stmt> <var_id> = <expression> ;
⇒ <stmt> <var_id> = <expression> + <expression> ;
⇒ <stmt> <var_id> = <expression> + <expression> + <expression> ;
⇒ <stmt> <var_id> = <expression> + <expression> + <var_id> ;
⇒ <stmt> <var_id> = <expression> + <expression> + y ;
⇒ <stmt> <var_id> = <expression> + <var_id> + y ;
⇒ <stmt> <var_id> = <expression> + x + y ;
⇒ <stmt> <var_id> = <constant> + x + y ;
⇒ <stmt> <var_id> = 3 + x + y ;
⇒ <stmt> z = 3 + x + y ;
⇒ <declaration_stmt> z = 3 + x + y ;
⇒ var <ident_list> ; z = 3 + x + y ;
⇒ var <var_id> , <ident_list> ; z = 3 + x + y ;
⇒ var <var_id> , <var_id> , <ident_list> ; z = 3 + x + y ;
⇒ var <var_id> , <var_id> , <var_id> ; z = 3 + x + y ;
⇒ var <var_id> , <var_id> , z ; z = 3 + x + y ;
⇒ var <var_id> , y , z ; z = 3 + x + y ;
⇒ var x , y , z ; z = 3 + x + y ; ✓
23 sentential forms.
Question: Given the following grammar,
<program> ::= <stmt_list>
<stmt_list> ::= <stmt> | <stmt> <stmt_list>
<stmt> ::= <declaration_stmt> | <assign_stmt>
<declaration_stmt> ::= var <ident_list> ;
<ident_list> ::= <var_id> | <var_id> , <ident_list>
<var_id> ::= x | y | z
<assign_stmt> ::= <var_id> = <expression> ;
<expression> ::= <expression> + <expression>
| <constant> | <var_id>
<constant> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
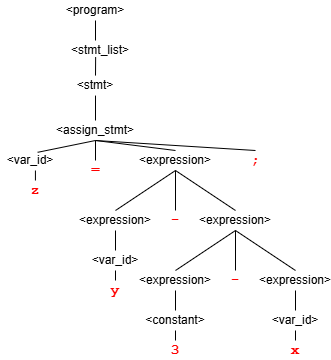
a) Give a parse tree for the string "z = 3 - x - y;".
b) Is the grammar ambiguous or not? Explain.
Answer:
a) The following is a parse tree for the string "z = 3 - x - y;".
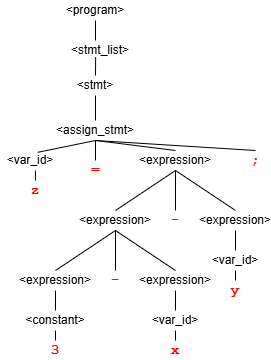
b) The following is also a parse tree for the same string. Since there are at least two different parse trees for the same string in the language of the greammar, the grammar is ambiguus.